(or cylindrical blobby bits on the end of stalks, if you prefer)
main page
This page was born after noticing a (cgt) post re a desire for a tool for making the above items. The requirement was for the user to be able to form a cylindical shape on the end of some sort of extrusion - where the extrusion end face essentially becomes one of the facets on the periphery of a cylindrical object..
Whilst there will be many approaches to this, including PutOn of a separate object, I've taken a basic geometry one - which might find uses outside this particular arena.
NB Always eyeball info readouts closely :)
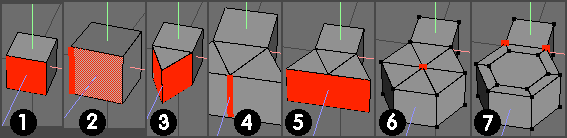
(Internal angle of the 'basic wedge apex' = 60 deg )
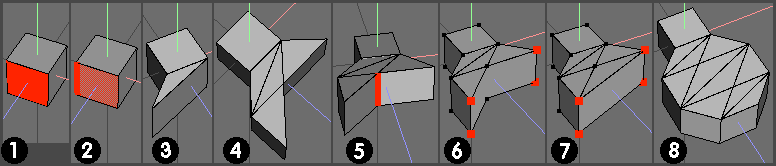
1). A cube face has been used to represent the extrusion end face.
Select a cube face and apply Face | Extract Normal -> 0 (zero) (constrain by holding down shift) - keep the extracted face selected.
(If preferred, loopcut the wedge at stage (3) to separate the 'wedge' from the 'stalk', rather than initially extracting a face and building a wedge on that.)
2). Apply Face | Lift (use LMB option) and select a suitable hinge edge for the operation. (I used a vertical one as the additional item will lie on a horizontal plane)
3). Execute Face | Lift to 60 deg (eyeball info readout and constrain using shift) to form the reference / datum wedge (equilateral triangle) and then select both new faces formed as shown.
4). Apply Face | Mirror (LMB) and select central edge after mirror op.
5). Dissolve selected edge and select resulting face (could also select both faces and dissolve :) )
6). Face | Mirror (LMB) to form a complete object, select centre verts (select one, press I) and apply Vert | Bevel to obtain configuration shown (if required).
7). Select both objects and apply Object | Weld to join together.
Using this method to create a hexagonal shape is simple (imo) because the Lift 60 deg step provides an equilateral triangle 'for free' as it were.
Cylindrical prisms with different numbers of sides require a little bit of maths in order to get the correct initial 'wedge' shape. The (additional) scaling operation basically alters the perpendicular height of the wedge triangle.
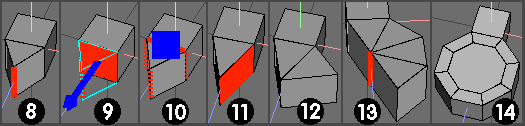
8). Use the same procedure as before to create a 60 deg 'wedge' This now has to be scaled to relocate the apex of the wedge for the appropriate number of facets required. Select the end vertical edge as shown.
9). Apply Edge | Scale (RMB option) and choose a suitable element to define the vector.
Various choices for this - in this example I'd previously selected the original face of the extrusion and saved this, using Store Selection and then recalled it - I have both on hotkeys. (don't use the extracted face, btw, as this gets rotated :) )
If the whole thing is aligned to an XYZ axis, use one of those - or, use the same selected end edge again (LMB) and press 2 to rotate the vector thro' 90 deg from the default setting - use whatever is most convenient :)
10). Accept this with Alt+RMB - because you want to set a reference origin for the distance to be scaled - I selected the upper edge (as shown) on the 'base' of the equilateral triangle - because the distance between the mid point of this edge to the apex of the triangle provides the perpendicular height of the triangular 'wedge'.
It is this 'height' that is going to be scaled.
11). Execute the scale op, press Tab (for numerical entry box) and enter 139.385 % (or 139.39 if you prefer, as easier to remember? ) This will produce the correct basic wedge for an octogon.
Select one face of this wedge.
12). Apply Face | Mirror (LMB) to get a 90 deg chunk.
13). Repeat Mirror op, remove central edge and do a final mirror to produce a complete object.
14). Weld and tidy up as before.
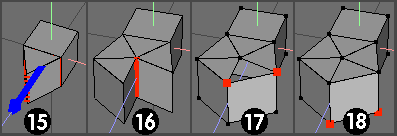
15). Same scaling procedure as before, but enter 79.465 % as the appropriate scaling factor to form the correct shaped wedge for a pentagonal prism.
16). Mirror (twice) to achieve this shape and select the central edge.
17). Dissolve edge, select verts and re-connect to 'close' last facet.
18). Repeat (17) with other pair of verts. (Then usual tidying, welding etc)
A similar procedure to this will be required for other shapes with odd numbers of sides.
Some scaling factors, compared with a hexagonal prism - choose the level of precision that offers the best compromise for the job in hand.
5 sides: 79.465 % (79.4654472 %)
7 sides: 119.888 % (119.8880187 %)
8 sides: 139.385 % (139.384685 %)
For shapes with more facets, work out the perpendicular height of the required 'wedge' and compare it with that for an equilateral triangle to get the scaling factor. (Ask at ODF if help reqd)
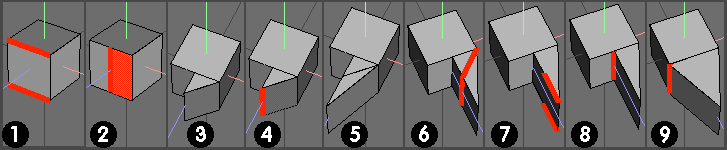
2). Connect edges, select one rectangular face and apply Face | Lift, choosing newly derived (connected) edge as hinge axis.
3). Execute Lift, dragging to 90 deg (use shift to constrain)
4). Repeat Lift operation with face and hinge edge shown (drag 135 deg)
5). Situation after second Lift op completed.
6). Select unwanted edges and dissolve.
7). Select edges shown and dissolve to remove intermediate verts (could use cleanup)
8). Select edge shown and re-position it as shown in (9). I used clacos' slide plugin (excellent and recommended) and used the weld option - alternatively, use scale to a point and cleanup afterwards. (See scale to a point page (here) for more details on this procedure if required)
9). Final wedge for an octogon - separate with loopcut, mirror to complete shape and weld back on. You could use an extracted face (as before) but loopcutting the extraction introduces new issues to be aware of - therefore loopcutting the wedge is easier (imo) this time :)
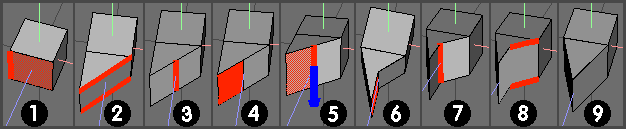
2). Apply Face | Lift -> 135 deg, using hinge axis shown.
3). After F. Lift.
4). Mirror triangular shape, then apply Lift (twice) to form the 2 additional triangular portions.
5). Select intermediate edge and dissolve.
6). Select verts shown and connect
7). After connecting verts, select face and mirror to complete shape.
8). Finished shape, tidy, weld etc etc.
2). Drag to 90 deg then select the 2 (diagonal) edges shown.
3). Apply Edge | Connect
4). Select face shown
5). Apply Face | Rotate (RMB option and select central edge as the rotate axis)
6). Rotate face 45 deg.
7). Select central edge and apply Edge | Dissolve.
8). Select edges shown and dissolve.
9). Final wedge for an octogon - Loopcut / mirror etc as before to obtain complete shape.
Because of the geometry involved it will be difficult to produce maths free methods for all shapes - but the scaling factor method will cope with anything (sensible).
In reality, for (relatively) low poly cages, I suspect that hexagons and octogons may well suffice anyway for many tasks?
For the record, the No2 method produces the most precise object - but I doubt that errors / tolerances (with the others) that are a few parts in a million will cause too much trouble with most models :)
As usual, I acknowledge the fact that there are many different approaches to this - the above is just something that I thought might be general interest (re the approach), as well as offering ideas for solutions to the particular problem.
pp