Edge | Cut > 10 (Note that Edge | Cut - N is now available in wings :)  ) main page
	Following a recent thread at ODF re cutting edges > 10 and especially to a prime number of equal parts I decided to add the info I posted here as well for reference..
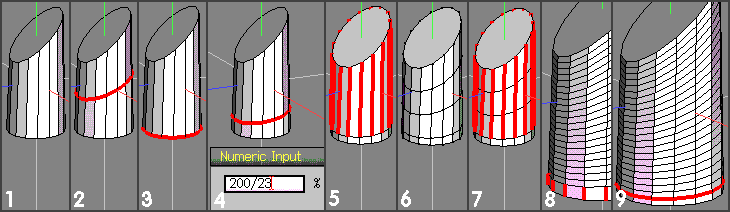
	Example to create 23 equi-spaced edgeloops. 1). Create cylinder as an example object - I also rotated X the top face to remove (some of) the uniformity. 2). Select all axial edges and connect them. 3). Apply Edge | Slide -> 100% Relative - so the edgeloop takes the shape of the edges around the lower face - accept this position. 4). Keeping this edgeloop selected, re-apply Slide (Relative), press tab to access the numeric entry box and enter 200/23 as shown. Why these numbers? I actually want to initially divide the edges into the proportion of 2:21 (total 23 portions) since 21 has factors of 3 and 7 (cut 3 and cut 7 already available on relevant hotkeys) So (2/23) * 100%. All I've done is to multiply 2x100 to save a step :) Accept the position and de-select. 5). Select all upper axial edges 6). Apply Edge | Cut 3 (press 3) - and connect the new verts 7). Select all edges produced in (6) and apply Edge | Cut 7 (press 7) - connect the new verts. 8). Situation after (7) - now got 21 of the 23 edges required. Select remaining short edges 9). Connect. I've assumed the new edgeloops were required as shown  / depicted - if not, mess around with Rel /Abs settings. Choose percentages (in 4) that make life as easy as possible. Eg for 13 sections, I'd suggest 5/13 (or similar) as both cut 5 and cut 8 already exist. Obviously, if the number of edges required can be achieved without using any of the above - don't bother :)
	A slightly different workflow to that described above will remove the second slide operation.  By using a single slide operation to adjust the newly connected central edgeloop (2), a position (for it) is achieved that allows the standard Cut 2->10 tools to be used. A table showing the data to be entered in the slide tab entry box to achieve this 'adjustment' is shown below, for all prime Nos between 10 -> 50 and multiples of same. This table does not (of course) show all possible variations - only those that (imo) provide 'sensible' positions that are are close to the original central edgeloop position. It's also possible that totally different proportions provide answers that require fewer subsequent Cut  (2->10) operations than those shown below - but it's a start :) 'Sensible' - eg - I see no point in sliding the loop to cut edges into a 22 : 1 ratio (for Cut 23 situation), as it leaves 2 prime No sections > 10 to be dealt with.
	Number of equal             Data for                Final proportions length edges needed        Tab box                 ( use Cut 2-> 10)         11                          100 / 11                 5 : 6         13                          100 / 13                 6 : 7         17                          100 / 17                 8 : 9         19                          100 / 19                 9 : 10                    22                          100 / 11               10 : 12         23                          500 / 23                 9 : 14         26                          100 / 13                12 : 14         29                          100 / 29                14 : 15         31                          100 / 31                15 : 16         33                          100 / 11                15 : 18         34                          100 / 17                16 : 18         37                          500 / 37                16 : 21         38                          100 / 19                18 : 20         39                          100 / 13                18 : 21         41                          100 / 41                20 : 21         43                          700 / 43                18 : 25         44                          100 / 11                20 : 24         46                          200 / 23                21 : 25         47                          700 / 47                20 : 27